核心要点:
- 在Excel中计算平方根对于几何、统计和金融至关重要,但传统方法需要掌握
SQRT()和POWER()等公式的技术知识。 - 匡优Excel提供了一个更简单的解决方案,通过使用纯语言指令即时执行平方根计算——无需公式语法。
- 与基于公式的方法相比,匡优Excel能轻松处理大型数据集和复杂的多步骤请求,无需手动设置和错误排查。
- 对于需要快速计算的商务人士来说,使用匡优Excel这样的AI工具意味着更快获得结果,并将更多时间用于分析而非技术实现。
计算平方根是数据分析中的一项基本任务,无论是用于几何问题、统计计算还是金融建模。Excel为此提供了强大的工具,但最佳方法取决于您的工作流程。
传统上,这意味着使用SQRT()等内置函数。它快速、可靠,并且易于集成到其他公式中。然而,现代的AI工具现在提供了一种完全不同的方法——使用纯语言而非语法。
在本指南中,我们将比较在Excel中求平方根的两种强大方法:经典的基于公式的方法,以及使用匡优Excel的现代对话式AI方法。
方法一:使用SQRT()的传统公式方法
在Excel中计算平方根最直接的方法是使用SQRT()函数。它专为单一目的设计:返回正数的正平方根。
SQRT()如何工作?
语法简单直接:
=SQRT(number)
其中,number可以是直接数值、单元格引用,甚至是另一个公式的结果。
何时应使用SQRT()?
任何需要计算正数的正平方根时,此函数都是可靠的选择。它常用于几何(例如根据面积求正方形的边长)、统计和金融领域。
基础SQRT()示例
让我们看看它在实践中如何工作。
求一个数的平方根
要计算25的平方根,您可以在任意单元格中输入:
=SQRT(25)
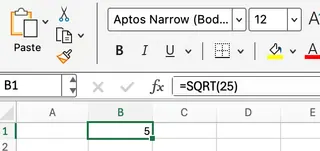
Excel正确返回5。这是进行更动态计算的基础。
使用单元格引用
在大多数电子表格中,您的数据不会是硬编码的。如果单元格A1包含数字81,您可以使用单元格引用:
=SQRT(A1)
此公式返回9。使用单元格引用使您的工作表具有动态性——如果A1中的值发生变化,结果会自动更新。
将SQRT()与其他公式结合
您还可以将计算直接嵌入SQRT()函数内部。例如,要求A1和B1之和的平方根:
=SQRT(A1 + B1)
当您的输入值源自其他数据点时,这很有用。
替代公式:POWER()
另一种计算平方根的方法是使用POWER()函数,该函数将一个数提升到给定的指数。由于平方根等同于将数字提升到0.5次幂,因此您可以使用:
=POWER(A1, 0.5)
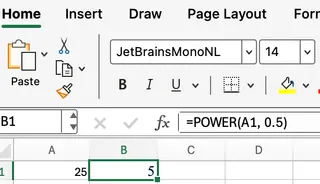
虽然这完全可行,但如果只需要平方根,SQRT(A1)更具可读性且更直接。在处理立方根或其他分数指数时,POWER()会更有用。
处理公式的错误和限制
SQRT()最大的限制是无法处理负数,因为负数的平方根不是实数。尝试计算=SQRT(-9)将导致#NUM!错误。
为避免这种情况,您可以使用IF()函数构建一个保护机制:
=IF(A1 < 0, "无效数字", SQRT(A1))
此公式首先检查A1中的数字是否为负数。如果是,则返回"无效数字";否则,继续进行计算。这很有效,但增加了公式的复杂性。
方法二:使用匡优Excel的AI驱动方法
如果能完全跳过公式会怎样?匡优Excel是一个Excel AI助手,允许您仅通过使用纯语言提问来执行计算、分析数据和创建图表。
您无需记住函数和语法,只需陈述您的请求。
匡优Excel如何工作?
过程非常简单:
- 将您的Excel文件上传到匡优Excel。
- 在聊天框中输入您的请求,就像与人类分析师交谈一样。
- 匡优Excel处理请求并即时交付答案、更新后的表格或图表。
要计算平方根,您可以上传一个在A列中包含数字列表的工作表,然后直接询问:
计算A列所有值的平方根,并将结果放入一个名为'平方根'的新列中。
匡优Excel会处理其余所有事情。无需输入公式,无需记住语法,也无需拖拽填充单元格。
何时应使用匡优Excel?
匡优Excel在公式变得繁琐的情况下表现出色。
- 对于初学者: 它消除了学习Excel函数库的障碍。
- 对于大型数据集: 单个命令可以处理数千行数据,省去了手动输入公式和拖拽的麻烦。
- 对于复杂请求: 您可以将命令链接在一起。例如,"计算A列的平方根,然后找出结果的平均值。"
- 对于错误处理: 匡优Excel可以理解上下文。如果您有负数,它可能会要求澄清或自动标记它们,避免出现使用
SQRT()时遇到的突兀的#NUM!错误。
方法比较:公式 vs. AI
| 特性 | 传统公式 (SQRT()) |
AI助手 (匡优Excel) |
|---|---|---|
| 易用性 | 需要了解函数语法 (=SQRT(A1))。 |
使用纯语言。无需语法。 |
| 速度 | 对于单次计算很快。对于大型数据集(拖拽填充)可能较慢。 | 对于单次计算和大型数据集都是即时的。 |
| 错误处理 | 返回#NUM!等错误。需要手动变通(例如,使用IF语句)。 |
更直观。可以标记问题或要求澄清。 |
| 灵活性 | 非常适合集成到复杂的嵌套公式中。 | 非常适合多步骤数据处理任务和无需设置的快速分析。 |
| 学习曲线 | 中等。您需要学习特定的函数及其限制。 | 极低。只要您能提问,就能使用它。 |
实际场景:正面比较
让我们重新审视我们的实际示例,看看这两种方法如何比较。
几何:计算正方形的对角线
您在A列有一个边长列表,需要求对角线。数学公式是 d = 边长 × √2。
SQRT()方法: 在单元格B1中,您需要输入=A1 * SQRT(2)并将公式向下拖拽填充整列。- 匡优Excel方法: 您只需询问:"对于A列中的边长,将每个乘以2的平方根,并在新的'对角线'列中显示结果。"
统计:计算标准差
标准差是方差的平方根。如果您在单元格B1中有方差:
SQRT()方法: 您需要输入=SQRT(B1)。当然,如果您知道的话,也可以使用专门的STDEV.P()或STDEV.S()函数。- 匡优Excel方法: 您可以跳过中间步骤,直接询问:"计算B列数据的标准差。" 匡优Excel理解统计概念,并执行正确的计算,而您无需知道底层公式。
结论:哪种方法适合您?
了解如何使用SQRT()和POWER()等函数是核心的Excel技能。它们让您能精细控制计算,并且对于构建复杂、相互关联的电子表格至关重要。对于快速的一次性计算或构建动态金融模型时,公式仍然是首选。
然而,数据分析的格局正在发生变化。像匡优Excel这样的AI助手引入了新的速度和可访问性水平。通过允许您使用自然语言,它们消除了记忆语法和构建复杂错误处理公式的需要。对于清理数据、执行多步骤分析,或者只是从电子表格中快速获取答案,AI方法通常更快、更直观。
最佳方法是两者兼用。掌握公式以获得控制力,并利用AI使您的工作流程更快、更智能。
准备好更快、更智能地计算了吗?立即试用匡优Excel,只需一个简单的请求即可执行平方根等复杂计算。








